[ 1 ] 트리란?
트리는 대표적인 비선형 자료구조이며 노드와 노드를 연결하는 에지를 통해 계층을 구성한다. 이때 트리의 중심이 되는 노드를 root라고 하며, 이 노드는 일반적으로 맨 위에 나타난다. 즉, 트리 구조를 그림으로 나타낼 때는 실제 나무와는 반대로 뿌리가 맨 위에 나타나게 되는 것이다. 트리를 통해 우리는 선형 자료구조로는 표현할 수 없는 계층적 문제를 표현할 수 있다.
[ 2 ] 이진탐색트리 (Binary Search Tree)
[ 2 - 1 ] 이진트리
이러한 트리 중에서도 각 노드가 최대 2개의 자식 노드만 가질 수 있는 '이진 트리'가 자주 활용되는데, 이진 트리에도
Complete Binary Tree, Full Binary Tree, Binary Search Tree, AVL Tree, Red-Black Tree 등 많은 종류가 있다.
그 중에서도 오늘은 Binary Search Tree에 대해 이야기 해 보고자 한다.
[ 2 - 2 ] 이진탐색트리의 속성
이진탐색트리의 대표적인 속성은 부모 노드보다 작거나 같은 모든 원소는 항상 왼쪽 sub tree에 있고, 부모 노드보다 크거나 같은 원소는 항상 오른쪽 sub tree에 있다는 점이다. 이러한 속성으로 인해 특정 원소를 검색하기 위해 root node부터 차례대로 값을 탐색하는 경우, 각 단계마다 검색 범위가 절반으로 줄어든다는 장점이 있다.
| - 부모 노드의 값 > 왼쪽 자식 노드의 값 - 부모 노드의 값 < 오른쪽 자식 노드의 값 |
[이진탐색트리 속성]

위의 트리는 모든 노드가 이진탐색트리의 속성을 지키고 있으므로 '이진탐색트리'이다.
[ 2 - 3 ] 이진탐색트리의 ADT
이진탐색트리의 ADT에는 search(), insert(), delete()가 있다. 다음은 세 함수를 구현하기 위한 Node 클래스이다.
#include <iostream>
using namespace std;
template<typename T>
class Node {
public:
Node<T>* left;
Node<T>* right;
T key;
Node(T _key)
{
this->key = _key;
this->left = NULL;
this->right = NULL;
}
};
(1) search() - 탐색
이진탐색트리에서 search() 는 root에서부터 탐색할 값을 비교하며 어느 하위 노드로 이동할지 결정해야 한다. 하위 노드 결정 방법은 이진탐색트리의 속성을 따르면 간단하다.
- 해당 트리의 root 값 > 내가 찾을 key 값 : 왼쪽 하위 노드로 내려간다.
- 해당 트리의 root 값 < 내가 찾을 key 값 : 오른쪽 하위 노드로 내려간다.
key 값을 찾을 때까지 해당 과정을 반복한다면 key 값을 찾거나, 혹은 찾지 못할 수도 있다.
template<typename T>
class BinarySearchTree {
private:
Node<T>* root;
public:
Node<T>* search(T _key)
{
return search_imp(root, _key);
}
private:
Node<T>* search_imp(Node<T>* current, T _key)
{
if(!current)
{
return NULL;
}
if(current->key == _key)
{
return current;
}
else if(current->key > _key)
{
return search_imp(current->left, _key);
}
else
{
return search_imp(current->right, _key);
}
}
}
(2) insert() - 삽입
이진탐색트리에서 새로운 원소를 삽입하면 항상 leaf node에 값이 저장되기 때문에 insert()하기 위해서는 원소가 삽입될 위치의 부모 노드를 찾아야 한다.즉, root부터 시작하여 각 노드를 추가할 원소와 비교하면서 원소가 삽입될 위치로 이동해야 하는 것이다.

만약 이 트리에 4를 삽입해야 한다면, root부터 시작하여 각 노드의 key값을 4와 비교하며 삽입될 위치를 찾는다.
- 4는 root의 key값인 12보다 작으므로 왼쪽 하위 노드로 이동한다.
- 4는 10보다 작으므로 왼쪽 하위 노드로 이동한다.
- 4는 8보다 작으므로 왼쪽 하위 노드로 이동하는데, 8의 왼쪽 하위 노드는 NULL이므로 4를 8의 왼쪽 하위 노드로 삽입한다.

- 4를 삽입한 결과는 다음과 같다.
template<typename T>
class BinarySearchTree {
private:
Node<T>* root;
public:
void insert(T _key)
{
if(!root)
{
root = new Node<T>(_key);
}
else
{
insert_imp(root, _key);
}
}
private:
void insert_imp(Node<T>* current, T _key)
{
if(current->key > _key)
{
if(!current->left)
{
Node<T>* newNode = new Node<T>*(_key);
current->left = newNode;
}
else
{
insert_imp(current->left, _key);
}
}
else
{
if(!current->right)
{
Node<T>* newNode = new Node<T>*(_key);
current->right = newNode;
}
else
{
insert_imp(current->right, _key);
}
}
}
}
(3) delete() - 삭제
이진탐색트리에서 원소를 삭제할 때는 세 가지 경우를 고려해야 한다.
| Case 1. 자식 노드가 없는 경우 | 해당 노드를 단순히 삭제한다. |
| Case 2. 자식 노드가 하나만 있는 경우 | 노드 삭제 후, 부모 노드의 포인터가 삭제 노드의 자식 노드를 가리키도록 조정 |
| Case 3. 자식 노드가 두 개 있는 경우 | 노드 삭제 후, 현재 노드를 후속 노드(successor)로 조정 |
Case1, Case2는 쉽게 이해할 수 있으나 Case3은 헷갈릴 수 있다. 후속 노드(successor)란 현재 노드 다음으로 큰 수를 가진 노드를 의미하며, 이는 현재 원소보다 큰 원소들 중에서 가장 작은 원소를 의미한다. 그러므로 후속 노드를 찾기 위해서는 삭제할 노드의 오른쪽 sub tree에서 가장 작은 노드, 즉 오른쪽 sub tree에서 가장 왼쪽에 위치한 노드를 찾아 삭제 노드를 대체해야 한다.

만약 해당 트리에서 root인 12를 삭제한다면, 12의 오른쪽 sub tree에서 가장 왼쪽에 있으며, 가장 작은 노드인 15로 12를 대체해야 한다.

12 삭제 결과는 다음과 같다. 즉, successor로 삭제 노드를 대체해야만 이진탐색트리의 속성을 유지할 수 있는 것이다.
다음은 delete()의 소스코드이며 successor를 찾는 함수도 추가했다.
template<typename T>
class BinarySearchTree {
private:
Node<T>* root;
public:
Node<T>* successor(Node<T>* start)
{
Node<T>* current = start->right;
while(current && current->left)
{
current = current->left;
}
return current;
}
void deletekey(T _key)
{
root = delete_imp(root, _key);
}
private:
Node<T>* delete_imp(Node<T>* node, T _key)
{
if(!node)
{
return NULL;
}
if(node->key > _key)
{
node->left = delete_imp(node->left, _key);
}
else if(node->key < _key)
{
node->right = delete_imp(node->right, _key);
}
else
{
// 자식 노드 없거나, 왼쪽만 없는 경우
if(!node->left)
{
Node<T>* temp = node->right;
delete node;
return temp;
}
// 오른쪽 자식 노드만 없는 경우
if(!node->right)
{
Node<T>* temp = node->left;
delete node;
return temp;
}
// case 3
Node<T>* succNode = successor(node);
node->key = succNode->key;
node->right = delete_imp(node->right, succNode->key);
}
return node;
}
}
[ 2 - 3 ] 이진탐색트리의 시간복잡도
만약, 이진탐색트리가 마지막 level을 제외한 모든 노드에 두 개의 자식이 있는 완전 이진 트리(complete binary tree)라면 트리의 높이가 log N이 되기 때문에 search, insert, delete의 시간복잡도는 O(log N)이 된다.
하지만, 이진탐색트리는 트리의 높이를 log N으로 유지하는 속성은 없기에 다음과 같은 worst case가 나타날 수 있다.
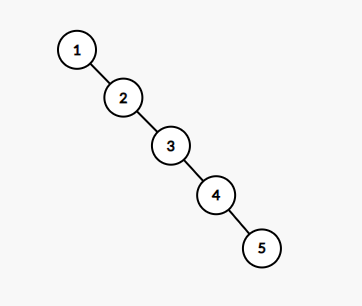
위는 1, 2, 3, 4, 5의 순서로 insert를 수행한 이진탐색트리이며, 이 경우 5를 탐색할 때 5번의 비교를 수행해야 하기 때문에 시간 복잡도가 O(N)이 된다.
즉, 이진탐색트리의 시간 복잡도는 항상 O(log N)이 아니고, 원소의 삽입 순서에 따라 O(N)이 될 수 있음을 유의해야 한다.
+ 추가) 항상 O(log N)의 시간 복잡도를 유지하는 트리로는 AVL Tree, Red-Black Tree 등이 있다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조/C++] 해시 테이블(hash table)과 체이닝(chaining) - vector와 list로 구현 (0) | 2022.07.13 |
|---|---|
| [자료구조/C++] 맵(map) (0) | 2022.07.11 |
| [자료구조/C++] 우선순위 큐 (0) | 2022.06.29 |
![[자료구조/C++] 이진탐색트리 (Binary Search Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbaBie1%2FbtrGrXpfKfV%2FyHQCxqyhccytLFjHQls291%2Fimg.png)